НЕПРЕРЫВНЫЕ, ДИСКРЕТНЫЕ И ЦИФРОВЫЕ СИГНАЛЫ, ТЕОРЕМА КОТЕЛЬНИКОВА.
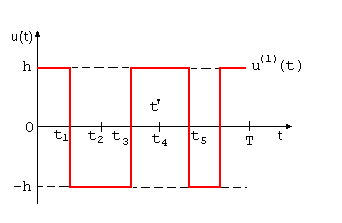
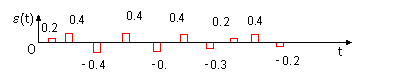
описываются непрерывными функциями времени. Мгновенные значения таких сигналов изменяются во времени плавно, без резких скачков (разрывов). Пример временной диаграммы непрерывного сигнала приведен на рис. 2, а. Сигналы, временные диаграммы которых изображены на рис. 1 , не являются непрерывными, поскольку их мгновенные значения в некоторые моменты времени изменяются скачками. Многие реальные сигналы являются непрерывными. К таковым можно отнести, например, электрические сигналы при передаче речи, музыки, многих изображений.

Рис. 1. График реализации телеграфного сигнала
. а)
а)
 б)
б)
 в)
в)
 г)
г)
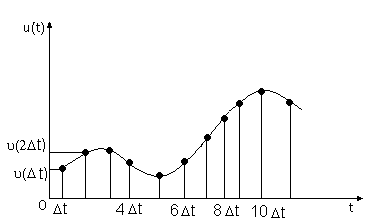
Рис. 2 Дискретизация квантование непрерывного сигнала
: а – непрерывный сигнал; б – дискретный по времени (импульсный) сигнал;
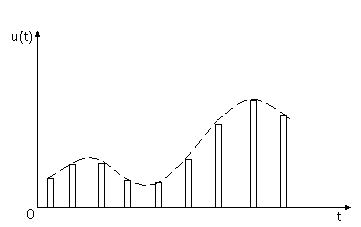
в – дискретный по времени и по значениям (цифровой) сигнал; г – ошибка квантования
.
Их можно получить из непрерывных, выполняя над последними специальное преобразование, называемое дискретизацией по времени. Смысл этих преобразований проиллюстрируем с помощью временных диаграмм, приведенных на рис. 2. Будем считать, что можно измерить мгновенные значения сигнала
u(t) в моменты времени Dt, 2Dt, 3Dt…; Dt называют интервалом дискретизации по времени. Измеряемые значения u(Dt), u(2Dt), u(3Dt) отмечены на рис. 2, а точками. По этим значениям можно сформировать последовательность коротких прямоугольных импульсов, длительность которых одинакова и меньше интервала дискретизации Dt, а амплитуды равны измеренным значениям сигнала u(t). Последовательность таких прямоугольных импульсов изображена на рис. 2, б и часто называется импульсным сигналом или сигналом с дискретным временем. Такой сигнал будет обозначать символом uд(t). Отметим, что шаг дискретизации по времени здесь постоянен и равен Dt, а амплитуда каждого импульса равна мгновенному значению сигнала u(t) в соответствующий момент времени. Поскольку непрерывный сигнал u(t) в выделенные моменты времени может принимать любые значения ; то и амплитуды импульсов импульсного сигнала; полученного из непрерывного путем дискретизации по времени; также могут принимать любые значения: На рис:2 ,б значения амплитуд импульсов указаны с точностью лишь до одного дисятичного знака после запятой; для точного указания значения амплитуд импульсов может потребоваться неограниченное число десятичных знаков после запятой, т:е: значения амплитуд импульсов заполняют непрерывно некоторый интервал. Поэтому амплитуды импульсов сигнала ид(t) иногда называют непрерывными величинами.
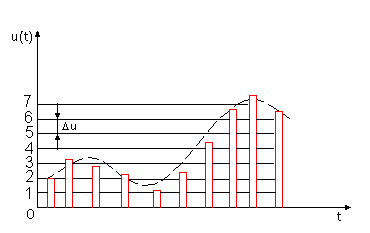
Как будет показано в дальнейшем, при передаче импульсных сигналов в электросвязи часто применяют специальное преобразование, состоящее в следующем. Предположим, что при передаче каждый импульс может иметь амплитуду лишь с разрешенным значением. Число разрешенных значений амплитуд импульсов конечно и задано. Например, на рис. 2,в разрешенные значения амплитуд пронумерованы цифрами 1, 2, 3, …;величина
D и равна разности между любыми двумя соседними разрешенными значениями амплитуд. Если истинное значение амплитуды импульса сигнала ид (t), подлежащее передаче, попадает между разрешенными значениями, то амплитуду передаваемого импульса принимают равной разрешенному значению, являющемуся ближайшим к истинному. Такое преобразование называют квантованием, совокупность разрешенных значений амплитуд передаваемых импульсов называют шкалой квантования, а интервал D и между соседними разрешенными значениями – шагом квантования. Например, на рис. 2,в разрешенные значения амплитуд импульсов приняты равными целым числам 0; 1; 2; 3 и образуют равномерную шкалу квантования, которая может быть продолжена и на область отрицательных значений сигнала и(t); при этом шаг квантования D и = 1.Последовательность импульсов, полученная в результате квантования импульсов сигнала ид
(t), также является импульсным сигналом, для которого введем обозначения иц(t). Особенность этого сигнала состоит в том, что амплитуды импульсов теперь имеют только разрешенные значения и могут быть представлены десятичными цифрами с конечным числом разрядов. Такие сигналы называют дискретными или цифровыми.Квантование приводит к ошибке квантования e(t) = uц(t) – ид
(t). На рис. 2,г Приведен пример временной диаграммы ошибки е(t). Передача цифрового сигнала иц(t) вместо сигнала ид(t) фактически эквивалентна передаче импульсного сигнала ид(t) с предварительно наложенным на него сигналом ошибки е(t), который в этом случае может рассматриваться как помеха. Поэтому е(t) часто называют помехой квантования или шумом квантования.
Теорема Котельникова.
Поскольку дискретные сигналы широко используют в настоящее время
при передаче сообщений, а многие реальные сигналы являются непрерывными, то важно знать, можно ли непрерывные сигналы представлять с помощью дискретных; можно ли указать условия, при которых такое представление оказывается точным. Ответы на эти вопросы дает доказанная в 1933 г. советским ученым В.А.Котельниковым теорема, являющаяся одним из фундаментальных результатов теоретической радиотехники. Это теорема формулируется следующим образом: если непрерывный сигнал и(t) имеет ограниченный спектр и наивысшая частота в спектре меньше, чем fв герц, то сигнал и(t) полностью определяется последовательностью своих мгновенных значений в дискретные моменты времени, отстоящие друг от друга не более чем на 1/ (2fв) секунд.Смысл теоремы Котельникова поясним с помощью временных диаграмм, приведенных на рис. 2,а. Пусть это будет часть временной диаграммы сигнала и(t) с ограниченным спектром и с верхней граничной частотой
fв. Если интервал дискретизацииD
t < 2 fв, то в теореме утверждается, что по значениям и(D t), u(2D t), u(3D t),…, отмеченным на рис.2.8,а точками, можно определить точное значение сигнала и(t) для любого заданного момента времени t, находящегося между моментами отсчета. В соответствии с этой теоремой сигнал с ограниченным спектром и верхней частотой w в Ј w д / 2 можно представить рядом![]()
где и(n
D t), n = …-1, 0, +1,… - отсчеты мгновенных значений сигнала и(t), w д = 2p fд , fд = Ѕ D t – частота дискретизации по времени.Ряд 2 имеет бесконечное число слагаемых, так что для вычесления значения сигнала и(t) в момент времени
t необходимо знать значения всех отсчетов и(nD t), n = …-1, 0, +1, …, как до, так и после указанного момента t. Точное равенство в (2) достигается, только когда учитываются все слагаемые; если ограничиться конечным числом слагаемых в правой части (2), то их сумма даст лишь приближенное значение сигнала и(t).Представление сигнала и(t) рядом (2) иллюстрируется с помощью рисунка 3, на котором изображены временные диаграммы сигнала и(t) и трех слагаемых ряда (2).
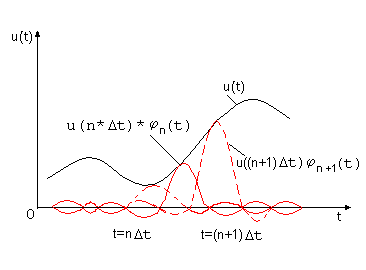
Рис. 3. Представление сигнала с ограниченным спектром рядом Котельникова.
Таким образом, теорема Котельникова указывает условия, при которых непрерывный сигнал может быть точно восстановлен по соответствующему ему сигналу с дискретным временем. Реальные непрерывные сигналы, подлежащие передачи, как правило, имеют спектры хотя и довольно быстро стремящиеся к нулю с ростом частоты, но все же неограниченные. Такие сигналы могут быть восстановлены по своим дискретным отсчетам лишь приближенно. Однако выбирая шаг дискретизации
Dt достаточно малым, можно обеспечить пренебрежимо малое значение ошибки восстановления непрерывного сигнала по его переданным отсчетам в дискретные моменты времени. Например, при передачи телефонного сигнала, спектр которого неограничен, обычно принимают, что условная верхняя граничная частота fв = 3,4 кГц. В этом случае получаем, что частота дискретизации должна удовлетворять неравенству fд і 6,8 кГц, т.е. в одну секунду должно передоваться 6,8 тысяч отсчетов. Качество передачи речи при этом оказывается вполне удовлетворительным. Увеличение частоты дискретизации сверх указанного значения допустимо и приводит к незначительному повышению точности восстановления телефонного сигнала. Если же принять fд < 6,8 кГц, то точность восстановления телефонного сигнала заметно падает.